Znalostní prostory

Příkladem je model vytvořený pro účely vzdělávání, avšak použitelný obecně (podobné modely se využívají i v umělé inteligenci), známý jako Knowledge Spaces Theory nebo jen Knowledge spaces (obvykle překládáno jako „znalostní prostory“).

Popis metody

Základní myšlenku modelu lze popsat příkladem: Představme si klasický didaktický test z matematiky sestávající z pěti položek dle tabulky 1. Je zřejmé, že prostá úroveň latentního faktoru „matematika“ získaná pomocí IRT nám příliš informací neposkytne. Ani kategorizace závislá na předem určeném a relativně malém počtu kategorií nemusí žákovy schopnosti popsat dokonale. Naopak detailní údaj, které položky v testu žák nezvládl (kupříkladu bb a dd), nám dá významně užitečnější informace (žák nezvládá dělení). Cílem je tedy podávat takto obsažné informace, avšak v jednodušší (a tedy snáze interpretovatelné) podobě, než je seznam (ne)vyřešených úloh. Navíc, jakožto u každého testování, chceme získat požadované informace s využitím minimálního možného počtu položek.


Tabulka 1: Příklad úloh.

Předpokládejme, že mezi odpověďmi žáka na jednotlivé položky existuje určitá závislost. Například můžeme předpokládat, že žák, který vyřeší úlohu c, dokáže vyřešit také úlohu a. Podobně pro úlohu e můžeme předpokládat dokonce vyřešení dvou úloh – a a c. Na základě tohoto předpokladu, respektive na základě výsledku pilotního testování, který by jej měl reflektovat, můžeme nad množinami úloh definovat částečné setřídění: Položka aa je větší než položka b, právě když položka aa implikuje položku b. Položka aa implikuje položku b, právě když všichni testovaní, kteří zodpověděli položku aa, zodpověděli také položku b, píšeme a→ba→b. Toto setřídění následně využijeme na konstrukci znalostního prostoru.

Pokud takto najdeme vztahy mezi všemi úlohami, nemusíme respondentovi pokládat všechny otázky, abychom zjistili, jaké jsou jeho znalosti nebo dovednosti. Příklad níže ukazuje možné setřídění úloh z tabulky 1. Obrázek 3 znázorňuje dobře sestavený rozhodovací strom, díky kterému můžeme předpovědět schopnost respondenta vyřešit všechny úlohy, i když mu položíme jen tři nebo čtyři z nich – nejprve se ho zeptáme na úlohu c. Pokud ji nedokáže vyřešit, můžeme předpokládat, že nevyřeší ani úlohu e, protože ta vyžaduje zvládnutí dovednosti, kterou zahrnuje už úloha c. Takto můžeme postupovat dále a i s menším počtem otázek získat přesnější informaci o řešitelových schopnostech, než by nám dávalo jen prosté celkové skóre z testu.

Nejprve definujme pojem knowledge state (neboli znalostní stav, stav znalostí). Knowledge state je množina vlastností (poznámka: například v našem případě položek, které je testovaný schopen vyřešit, ale nejedná se nutně o množinu položek; vlastností můžeme v tomto kontextu rozumět také množinu položek odpovídající určité kompetenci, tedy přeneseně onu kompetenci apod.), v našem jednoduchém případě tedy množina položek {ace}. Množina stavů znalostí může tvořit znalostní prostor (knowledge space). Znalostní prostor příslušný dané relaci je množina stavů znalostí, která je uzavřená na sjednocení, obsahuje prázdný stav znalostí a úplný stav znalostí (množinu všech vlastností dané domény) a respektuje tuto relaci. To znamená, že pro každý stav znalostí SS v tomto znalostním prostoru a každou úlohu domény platí:

$ a\in S \wedge a \rightarrow b \Longrightarrow b \in S $

Znalostní prostor je opět částečně uspořádanou množinou na základě relace podmnožiny. Dobře stupňovaným (well-graded) znalostním prostorem nazveme takový znalostní prostor, kde pro každé dva znalostní stavy z tohoto prostoru A a B, kde A⊂BA⊂B existuje sekvence znalostních stavů $ C_{0}=A\subset C_{1}\subset C_{2}\subset\ldots\subset C_{k}=B $ z daného prostoru taková, že každé dva po sobě následující stavy Ci, Ci+1 se od sebe liší právě jednou vlastností.

Modelem dané domény je potom dobře stupňovaný znalostní prostor příslušný relaci této domény. Pomocí tohoto modelu potom můžeme vytvořit test, například v podobě rozhodovacího stromu, který určí přesnou polohu testovaného v modelu a tím nám umožní přesně popsat jeho vlastnosti.

Příklad

Pro demonstraci si ukažme příklad, jak by takové setřídění úloh, příslušný znalostní prostor a rozhodovací strom mohly vypadat.


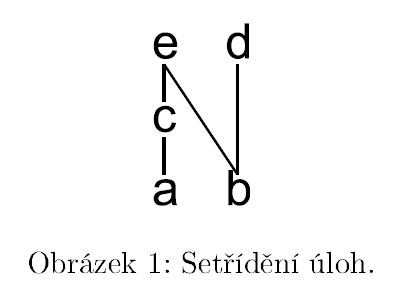
Obrázek 1 ukazuje možné setřídění úloh vycházející z tabulky 1.


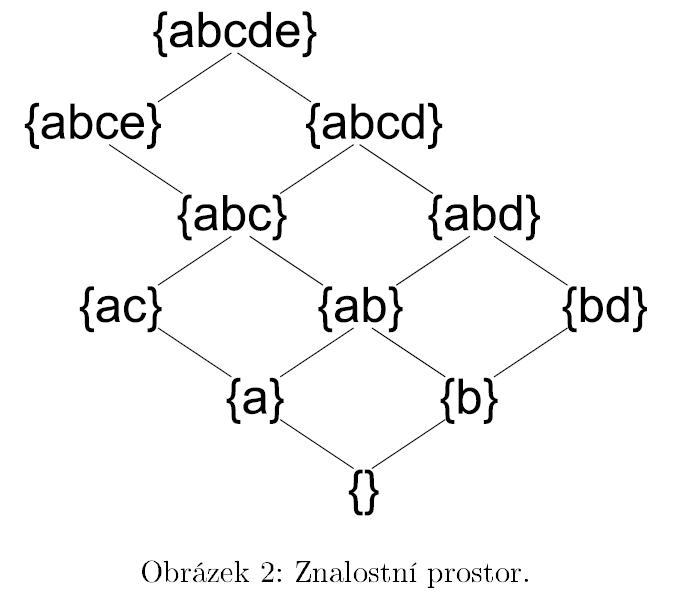
Obrázek 2 potom zobrazuje příslušný dobře stupňovaný znalostní prostor včetně jeho struktury (ve složených závorkách je uveden seznam úloh, které testovaný nacházející se v tom kterém stavu je schopen řešit).

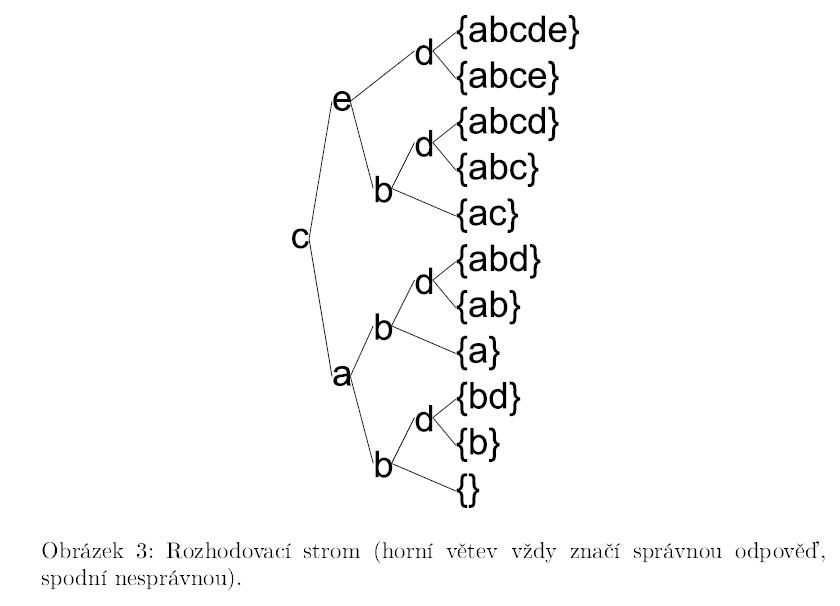
Na obrázku 3 je zobrazen příklad deterministického adaptivního testu ve formě rozhodovacího stromu, který určí znalostní stav testovaného.

---

Reference:
J. Dvořák: Moderní způsoby tvorby a vyhodnocování testů. In Proc. Meranie vedomostí ako súčasť zvyšovania kvality vzdelávania, Trnava, Slovensko, 2011