Statistické pojmy

Normální rozdělení

Z každodenní zkušenosti vyplývá, že pro řadu jevů nebo náhodných veličin (pokusů) je typické podobné rozložení možných výsledků: nejčastější výsledky se pohybují kolem průměru, výsledky vzdálenější od průměru se objevují řidčeji; přitom se přibližně stejně často objevují výsledky nadprůměrné i podprůměrné (tj. rozložení je symetrické kolem průměru). Takové rozložení výsledků vystihuje tzv. normální rozdělení, které je základním rozdělením pravděpodobností náhodných veličin.

Graf 1 Hustota normálního rozdělení

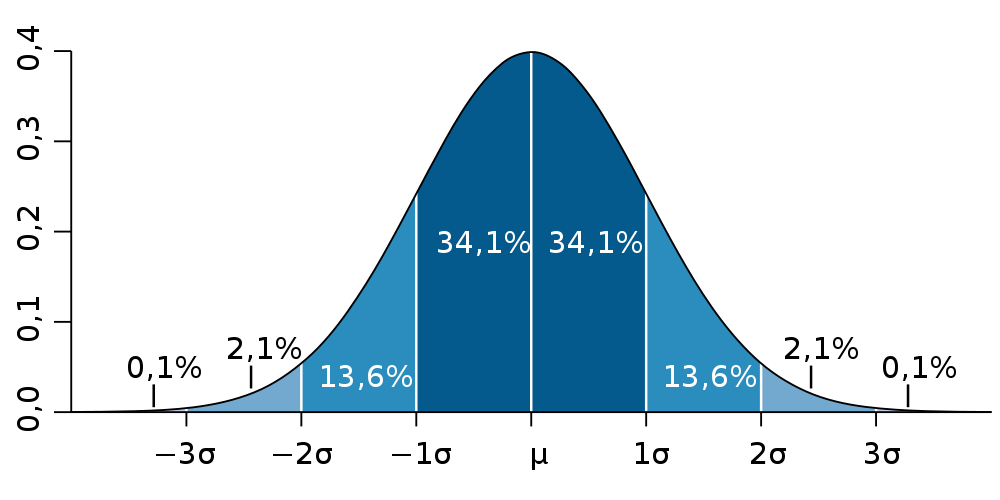
Zdroj: Wikipedia; Autor: Petter Strandmark, upravil Nusha (desetinné čárky)

V Grafu 1 je znázorněna tzv. hustota normálního rozdělení se střední hodnotou rovnou μ a směrodatnou odchylkou rovnou σ. Normálnímu rozdělení s takovými parametry se říká též standardní normální rozdělení. Hustota schematicky popisuje, v jakých oblastech (osy x) je výsledek náhodného pokusu s normálním rozdělením více pravděpodobný a v jakých méně. Je zřejmé, že nejpravděpodobnější výsledky jsou poblíž μ (tj. poblíž střední čili průměrné hodnoty). Naprostá většina výsledků (přibližně 95 %) se pak vyskytuje v rozmezí od –2σ do 2σ. Z toho vychází i tzv. pravidlo 2σ (viz kapitola Rozptyl a směrodatná odchylka).

Hustota normálního rozdělení se označuje též jako Gaussova křivka.

Vážený průměr

V některých situacích nelze použít obvyklý aritmetický průměr hodnot X1,X2 až Xn podle známého vzorce

\( \bar{X} = \frac{X_1 + X_2 + \dots + X_n}{n} \)

Stává se to tehdy, když jednotlivé prvky, z nichž má být průměr vypočten, nemají stejnou důležitost, jsou založeny na různých počtech pozorování apod. Příkladem může být výpočet celkové průměrné známky školy v matematice, jsou-li známy průměry všech tříd, avšak třídy jsou různě početné. V takovém případě se používá vážený průměr, který bere v úvahu různou důležitost (tj. váhu) jednotlivých prvků. Důležitost čili váha se vyjadřuje pro každý prvek kladným číslem w1, w2.., čím vyšší důležitost, tím vyšší číslo. Výsledný vážený průměr se pak vypočítá pomocí vzorce

\( \bar{X}_{\text{vážený}} = \frac{w_1 X_1 + w_2 X_2 + \dots + w_n X_n}{w_1 + w_2 + \dots + w_n} \)

Rozptyl a směrodatná odchylka

Tyto dvě veličiny vyjadřují, jak se hodnoty z určitého souboru odchylují od svého průměru – tedy jak moc jsou rozptýlené. Rozptyl (někdy též označovaný jako disperse či variance) se vyjadřuje jako průměr druhých mocnin odchylek od průměru, tj.

\( \mathrm{var}(X) = \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X})^2 \)
je soubor hodnot

Pokud hodnoty X1, X2... nejsou úplným souborem hodnot, nýbrž jen výběrem z tohoto souboru, nelze spočítat přesný rozptyl, ale jen odhad rozptylu. K tomu se používá velmi podobný vzorec

\( S^2 = \frac{1}{n - 1} \sum_{i=1}^{n} (X_i - \bar{X})^2 \)

Směrodatná odchylka je druhou odmocninou rozptylu. Je pro praktický odhad rozmístění hodnot důležitější než rozptyl, neboť v mnoha případech lze aplikovat tzv. pravidlo 1σ, resp. pravidlo 2σ:

Pravidlo 1σ: přibližně dvě třetiny všech hodnot souboru se od průměru liší nejvýše o jednu směrodatnou odchylku.
Pravidlo 2σ: přibližně 95 % všech hodnot souboru (resp. „téměř všechny hodnoty“) se od průměru liší nejvýše o dvě směrodatné odchylky.

z-skór a T-skór

Pokud pozorujeme několik znaků, které mají různé škály, bývá vhodné převést jejich hodnoty na některou standardizovanou škálu. Základní transformací je tzv. z-transformace:

z-skór = (původní hodnota – průměrná hodnota) / směr. odchylka hodnot

Z-transformace je lineární transformací, a proto škálu pouze posunuje a rovnoměrně mění měřitko, nedeformuje vzdálenosti mezi hodnotami. Průměr z-skórů je 0 a jejich směrodatná odchylka 1. Z-skóry ovšem nabývají desetinných hodnot a mohou být i záporné, takže se hůř interpretují. Proto se z-skóry někdy transformují ještě dále na vhodnější škálu, například pomocí T-transformace:

T-skór = 50 + 10 x z-skór

T-skóry mají průměr 50 a směrodatnou odchylku 10, nabývají tedy nejčastěji hodnot mezi 20 a 80.

Stejně tak je možné převádět standardizované skóre i na jiné stupnice. Populární je například škála, na které se udává IQ a která má průměr 100 a směrodatnou odchylku 15, mezinárodní testování PISA zase používá škálu s průměrem 500 a směrodatnou odchylkou 100.

Šikmost a špičatost

Tyto méně obvyklé charakteristiky slouží k vystižení dalších vlastností rozložení hodnot souboru. Šikmost zjišťuje, zda jsou hodnoty rozloženy okolo průměru symetricky, špičatost pak porovnává koncentraci hodnot blízko průměru a dále od něho.

Graf 2

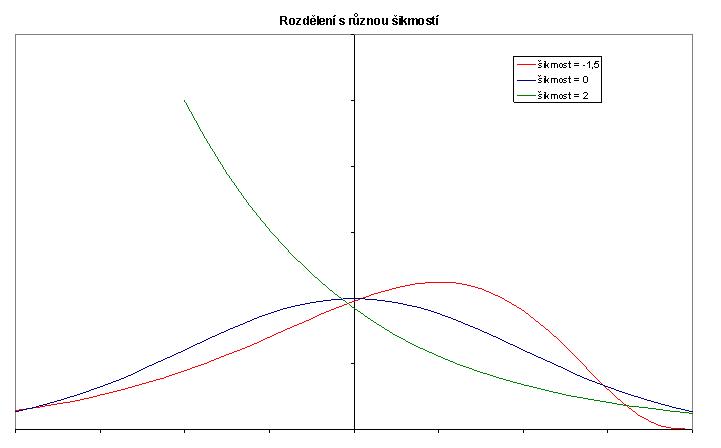
V Grafu 2 jsou uvedeny tři křivky vystihující rozložení hodnot. Všechna tři rozložení přitom mají stejný průměr (ten leží v místě svislé osy).

Křivka, která je zcela symetrická, má šikmost rovnu nule – to je případ modré křivky. Zelená hladká křivka vystihuje rozložení, kdy hodnoty pod průměrem mohou být nejvýše o 2 jednotky menší než průměr (dokonce hodnoty kolem dvou jednotek pod průměrem jsou nejpravděpodobnější), zatímco nad průměrem se vyskytují i hodnoty o 4 jednotky vyšší (i když s nevelkou pravděpodobností). Takové rozložení má kladnou šikmost, neboť výskyt nadprůměrných hodnot značně vzdálených od průměru je pravděpodobnější než výskyt vzdálených podprůměrných hodnot. Opačně je tomu u červené křivky: pravděpodobnější jsou podprůměrné vzdálené hodnoty, a šikmost je tak záporná.

Graf 3

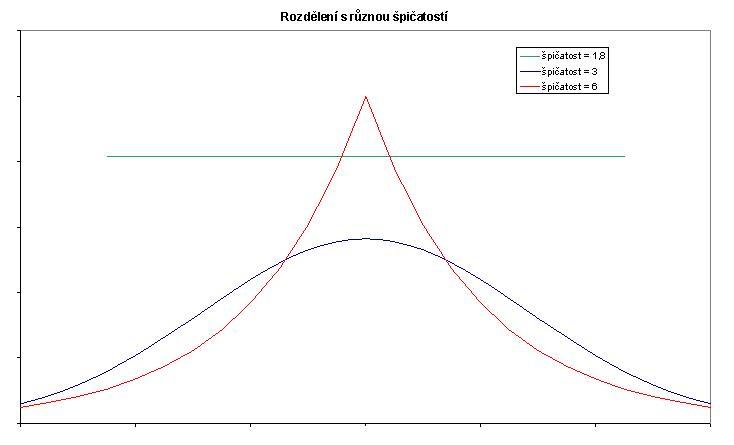
Pomocí špičatosti můžeme zjistit, zda a do jaké míry jsou hodnoty koncentrovány poblíž průměru. Modrá křivka odpovídá normálnímu rozdělení (jde o tzv. Gaussovu křivku, viz kapitola Normální rozdělení) a špičatost je rovna 3. Tato hodnota je tedy referenční pro porovnání, zda nějaké rozložení hodnot odpovídá normalitě. Menší špičatost má rovnoměrné rozložení popsané zelenou hladkou čarou, naopak větší špičatost vykazuje rozložení popsané červenou křivkou s ostrým vrcholem.

Medián, kvartil, decil, percentil

Kromě aritmetického průměru, směrodatné odchylky (či rozptylu), šikmosti a špičatosti lze rozložení hodnot nějakého souboru popsat i dalšími charakteristikami. Pokud hodnoty uspořádáme podle pořadí, může být důležitou informací, která hodnota je právě uprostřed, která v jedné desetině či čtvrtině celkového pořadí. Tento přístup vede k určení charakteristik uvedených v nadpisu.

Medián je hodnota nacházející se právě uprostřed pořadí. Nad mediánem se tedy vyskytuje stejně tolik hodnot, kolik pod mediánem.
Dolní, resp. horní kvartil je hodnota nacházející se v jedné čtvrtině pořadí, resp. ve třech čtvrtinách pořadí. Pod dolním kvartilem se tedy vyskytuje jedna čtvrtina všech ostatních hodnot a nad ním tři čtvrtiny všech ostatních hodnot. U horního kvartilu je to obráceně.
První, druhý až devátý decil je hodnota nacházející se v jedné, dvou atd. až devíti desetinách pořadí. Například pod sedmým decilem se vyskytuje 70 % všech ostatních hodnot a nad ním jen 30 % ostatních hodnot. Pátý decil je shodný s mediánem.
Percentily jsou obdobou decilů, pouze se nevztahují k desetinám, ale k setinám pořadí.

Z uvedených charakteristik lze odvodit i další, například tzv. kvartilové rozpětí je rozdíl mezi horním a dolním kvartilem.

Korelace

Máme-li k dispozici soubor několika jedinců, můžeme na každém z nich pozorovat různé znaky či veličiny (u lidí např. výšku, váhu, výsledek v nějakém testu či odpovědi na otázky v dotazníku). Častým problémem je, zda jsou hodnoty určité dvojice znaků na sobě nezávislé, nebo zda vyšší hodnota jednoho znaku vede zpravidla k vyšší (nebo nižší) hodnotě druhého znaku. Existuje řada metod, jak nezávislost dvojice znaků ověřit, jednou z nich je výpočet korelace.

Tato metoda je použitelná tam, kde každý z dvojice znaků nabývá buď číselných (kvantitativních) hodnot, anebo aspoň takových kvalitativních hodnot, které lze logicky uspořádat (např. stupeň dosaženého vzdělání nebo míra spokojenosti či souhlasu s nějakým výrokem). Principem výpočtu korelačního koeficientu je zjištění, zda dvojice sledovaných znaků nabývá často zároveň nadprůměrných či zároveň podprůměrných hodnot (souhlasná čili kladná korelace); nebo zda jsou hodnoty často na opačných stranách od průměru (nesouhlasná čili záporná korelace); případně zda se stejné i různé vzájemné polohy obou znaků vůči průměru vyskytují přibližně stejně často (žádná korelace, nekorelovanost).

Matematicky se korelace vyjadřuje číslem mezi –1 a 1. Hodnoty blízké nule signalizují nekorelovanost veličin, hodnoty dále od nuly pak kladnou nebo zápornou korelaci podle znaménka vypočteného koeficientu. Jak vysoké hodnoty odpovídají silné či slabé korelaci, záleží na konkrétní situaci, korelace nad 0,5 či pod –0,5 se však obecně považují za silné.

Přítomnost korelace nemusí automaticky znamenat příčinnou závislost veličin. Korelaci totiž může způsobovat třetí veličina, která ovlivňuje obě dvě. Například mezi počtem úrazů a počtem prodaných rohlíků v městech ČR existuje korelace, která je však způsobena závislostí obou těchto veličin na počtu obyvatel obce. Pokud počítáme korelaci se zafixovanou hodnotou třetí proměnné, hovoříme o tzv. parciální korelaci.

Statistická významnost a testování hypotéz

Provádí-li se pokus, jehož výsledek ovlivňuje náhoda, existuje zpravidla mnoho možných výsledků pokusu. Některé výsledky mohou sice nastat, ale jejich pravděpodobnost je tak malá, že jejich nastání by bylo podezřelé. Například při deseti hodech hrací kostkou je možné, avšak velmi málo pravděpodobné, že ve všech deseti případech padne šestka. Takový jev by byl velmi nečekaný a vzbudil by podezření, že se při pokusu podvádělo. Naopak pokud by z deseti pokusů padla dvakrát jednička, dvakrát dvojka, dvakrát pětka, dvakrát šestka a po jedné trojce a čtyřce, vypadal by takový výsledek přirozeně a žádné podezření by nevzbudil.

Na právě popsané úvaze je založen princip statistického testování hypotéz a pojem statistické významnosti, resp. statisticky významného rozdílu. Před pokusem (či před analytickým výpočtem) se přijme určitý předpoklad – zpravidla takový, že zkoumaná veličina má určitou střední (průměrnou) hodnotu nebo že se zkoumané dvě veličiny mezi sebou neliší. Pokus je zkonstruován tak, aby v případě, že je předpoklad splněn, dal „rozumný“ výsledek, kdežto při porušení předpokladu by měl dát „podezřelý“ výsledek. A podle toho, zda pokus přinese „rozumný“ nebo „podezřelý“ výsledek, se rozhodne, zda učiněný předpoklad byl přijatelný, nebo zda je třeba jej odmítnout.

Odmítnutí předpokladu se často interpretuje jako existence statisticky významného rozdílu. Pokud se například předpokládala shoda dvou veličin, „podezřelý“ výsledek pokusu znamená, že předpoklad o rovnosti dvou veličin byl nesprávný. Říká se pak, že „mezi veličinami je statisticky významný rozdíl“. Obdobně pokud se ověřuje, zda střední (průměrná) hodnota veličiny je rovna danému číslu X, výsledek se interpretuje jako „veličina se liší/neliší statisticky významně od čísla X“.

Reliabilita

Měření či jiné zjišťování hodnoty veličiny je v praxi často zatíženo chybou. Tato chyba může být malá, například při použití velmi přesného měřicího přístroje, anebo velká, například při nedbalém měření či při chybném odečtení hodnoty ze stupnice. Jelikož testování je také měření určitého druhu (měření žákových znalostí a schopností), je žádoucí znát nebo aspoň odhadnout jeho přesnost, aby bylo možné stanovit, do jaké míry se lze na výsledek měření spolehnout a na základě něho vyvozovat důsledky.

U testů tuto informaci poskytuje do značné míry reliabilita. Tato charakteristika vyjadřuje, jak velká část z variability výsledků účastníků připadá na rozdílné úrovně znalostí a schopností účastníků a jaká část variability je daná vlivem náhody či chybou měření. Reliabilita se vyjadřuje jako číslo mezi 0 a 1. Hodnoty blízké jedné znamenají, že vliv náhody je minimální a výsledky testu dobře odpovídají skutečným znalostem a schopnostem účastníků. Naopak příliš nízké hodnoty reliability signalizují, že do výsledků silně promlouvají náhodné vlivy.

Reliabilita má velký význam v situaci, kdy lze předpokládat, že výsledky všech účastníků jsou zatíženy přibližně stejně velkou chybou. V takovém případě je možné na základě velikosti reliability a směrodatné odchylky výsledku účastníků určit pro každého účastníka tzv. střední chybu měření. Pomocí střední chyby pak získáme rozpětí, v němž se nachází výsledek odpovídající skutečným znalostem a schopnostem každého žáka. Pokud nelze předpokládat přibližně stejně velkou chybu u všech žáků, má reliabilita hlavně informativní hodnotu.

Často se hodnoty reliability srovnávají s doporučenými hodnotami pro určité účely.

test s reliabilitou nad 0,9 se pokládá za dostatečný k tomu, aby výhradně na jeho základě bylo možné činit rozhodnutí (např. o přijetí či nepřijetí),
test s reliabilitou mezi 0,8 a 0,9 je vyhovující jako jeden z podkladů pro rozhodnutí
test s reliabilitou mezi 0,6 a 0,8 je na individuální úrovni nepostačující pro rozhodování, avšak pro rozhodování o malých skupinách (do 10 osob) je postačující

Pro rozhodování o větších skupinách (např. na úrovni tříd a škol) jsou na reliabilitu kladeny mnohem menší nároky, daleko důležitější je spolehlivost dosažených výsledků (zamezení opisování a napovídání, dodržení zásad administrace testu atd.).

Skutečnou hodnotu reliability lze vypočítat jen za splnění speciálních předpokladů, zpravidla je třeba ji pouze odhadnout. Nejpoužívanějšími odhady jsou výpočty korelace výsledků účastníků ve dvou různých polovinách testu (tzv. split-half reliabilita) a výpočet vnitřní konsistence testu (Cronbachovo alfa a speciální vzorec KR-20, nověji též přesnější odhad koeficientem L2).

Item-response theory, Raschův model

Každé testování, které používá víc než jedno testové zadání, se potýká s problémem, jak zaručit srovnatelnost výsledků. Touto problematikou se začala významně zabývat až moderní teorie testování (IRT, item-response theory).

V klasické teorii testování se úspěšnost žáků a obtížnost testových položek vyjadřuje v procentech, resp. jako podíl z maximálního možného počtu bodů či maximální možné úspěšnosti (pojem „testová položka“ se v literatuře o teorii testování používá místo obvyklého pojmu „úloha“. Obvykle lze ovšem oba pojmy zaměnit.). Tyto ukazatele jsou názorné a snadno pochopitelné i interpretovatelné, ovšem vztahují se ke konkrétnímu zadání či konkrétní skupině účastníků testování. Vymění-li se totiž v testu některé úlohy, dosáhnou stejní žáci odlišné úspěšnosti; vymění-li se pro stejný test někteří účastníci, bude obtížnost testových položek odlišná.

Moderní IRT se pokouší stanovit pro každou testovou položku stálou charakteristiku obtížnosti položky a pro každého žáka stálou charakteristiku úrovně schopností. K tomu účelu zavádí omezující předpoklad, tzv. charakteristickou křivku položky. Tato křivka vyjadřuje, jaká je pravděpodobnost, že žák s danou úrovní schopností položku vyřeší. Charakteristická křivka vychází z průběhu tzv. logistické funkce, obecný tvar je

\( P(\theta) = c + (1 - c) \cdot \frac{1}{1 + e^{-a(\theta - b)}} \)

kde a je citlivost neboli diskriminace položky (libovolné reálné číslo),
b je obtížnost položky (libovolné reálné číslo, ale v praxi v rozmezí –4 až 4),
c je parametr uhodnutí (0 <= c <= 1, v praxi 0 <= c <= 0,5),
theta je úroveň schopností žáka (libovolné reálné číslo, ale v praxi v rozmezí –4 až 4).

Graf 4 znázorňuje příklad charakteristické křivky testové položky pro a=1, b=–1 a c=0,25.

Graf 4

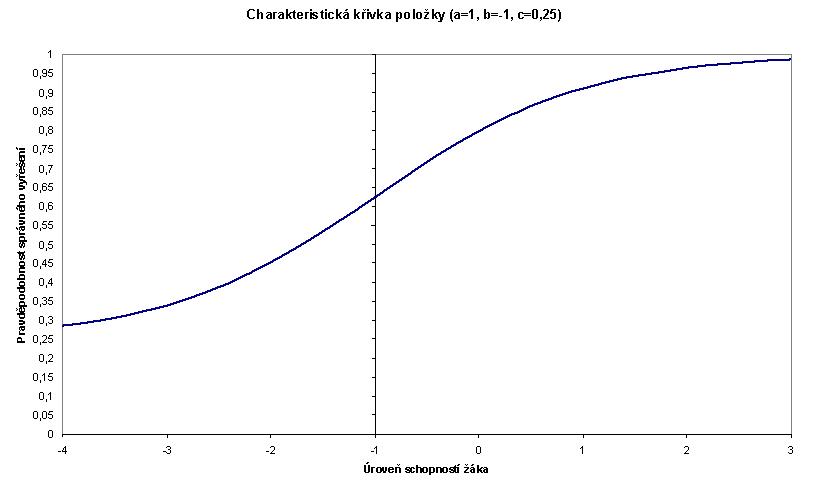
Průběh charakteristické křivky ukazuje, že čím má žák vyšší úroveň schopností, tím je větší pravděpodobnost, že danou testovou položku správně vyřeší. Naopak pro žáky s nízkou úrovní schopností se pravděpodobnost zmenšuje. Přitom však i pro nejhorší žáky zůstává pravděpodobnost nejméně 0,25, neboť to je pravděpodobnost náhodného uhodnutí správného řešení (aplikuje se u uzavřených úloh s výběrem z nabídky odpovědí).

V praxi se někdy používá pouze model s jedním parametrem, kterému se říká též Raschův model. K tomuto modelu dospějeme tím, že pevně stanovíme a=1 a c=0. Raschův model tedy předpokládá stejnou citlivost všech položek a nemožnost uhodnout správné řešení.

Aplikací IRT je možné např. sestavit různé verze testů tak, aby výsledky žáků bylo možné převést na stejnou škálu, a tím vzájemně porovnat. Rovněž bylo možné porovnat výsledky testování v letech 2003 a 2000. Je ovšem nutné, aby odpovědi respondentů odpovídaly modelu, např. aby byly z velké části ovlivněny jedním latentním faktorem.

Odhad výsledku metodou maximální věrohodnosti a pomocí možných hodnot (plausible values)

Jak vyplývá z kapitoly Item-response theory, na rozdíl od obvyklého školního testování je pro srovnatelnost vhodnější uvádět výsledek žáka jako úroveň schopností. Absolutní počet získaných bodů či úspěšnost, z nichž se úroveň schopností odvozuje, lze sice uvést také, ovšem bez informace o obtížnosti celého testu to může být zavádějící údaj (dva žáci mohou mít v různých testech stejný bodový výsledek; avšak jsou-li tyto testy různě obtížné, přirozeně se liší i úroveň schopností těchto žáků.).

Úroveň schopností se odvozuje z výsledku v testu pomocí tzv. metody maximální věrohodnosti. Tato metoda je obecným a často používaným způsobem, jak odhadnout hodnotu určitého parametru v matematickém modelu. Podstatou metody maximální věrohodnosti je následující úvaha.

Výkon žáka v testu je ovlivněn zčásti jeho skutečnými znalostmi a schopnostmi, zčásti náhodnými vlivy. Je přitom logické, že žák s menšími schopnostmi pravděpodobně dopadne v testu hůře než žák s lepšími schopnostmi. Jinak řečeno, pro každou skutečnou úroveň žákových schopností je určitý výsledek v testu nejpravděpodobnější, jiné výsledky méně pravděpodobné a ještě jiné téměř nemožné. V praxi sice skutečnou úroveň schopností žáka neznáme, známe však výsledek v testu. Metoda maximální věrohodnosti vychází z předpokladu, že žák v testu dosáhl toho výsledku, který je pro jeho skutečnou úroveň nejpravděpodobnější. V praxi to tedy znamená, že se ze všech možných hodnot úrovně schopností vybere ta, pro niž je nejpravděpodobnějším výsledkem právě dosažený výsledek v testu.

Při použití zmíněného postupu je nutné vzít v úvahu dvě důležité věci:

Metoda maximální věrohodnosti může poskytovat vychýlené odhady.
Zatímco skóre v testu je zřejmé a snadno spočitatelné (samozřejmě s vědomím, že žádné testování není absolutně přesné ), úroveň schopností se pouze odhaduje. To je dalším zdrojem variability a zejména při individuálním rozhodování o žákovi může nepřesnost tohoto odhadu být fatální (při obvyklém „školním“ testování se dosažené výsledky žáků často mylně považují za naprosto přesné, ačkoliv je známo, že do výsledku jakéhokoliv testování se promítá v různé míře náhoda a jeho výsledky jsou do nějaké míry nepřesné. Jinými slovy, pokud například žák dosáhne v testu 70 bodů ze 100 možných, je to jen přibližné vyjádření jeho skutečných schopností a při posunu testování o den později by získal třeba 68 nebo 73 bodů).

Jinou nevýhodou úrovně schopností je to, že může nabývat i záporných hodnot – v praxi obvykle od –4 do 4. Proto se úrovně schopností transformují tak, aby průměrná hodnota nebyla 0, ale 50, 100 nebo 500, a aby směrodatná odchylka činila 10, 20 nebo 100. Naprostá většina výsledků žáků se pak pohybuje mezi hodnotami 30 a 70 (resp. 60 a 140 nebo 300 a 700), tudíž lze přirozeně hovořit o výsledku v „bodech“ (narozdíl od původních hodnot, kde „záporné body“ či desetiny a setiny bodů jsou pro laiky velmi nezvyklé).

Transformací přitom nejsou deformovány vztahy mezi výsledky žáků, takže všechny analýzy lze na původních i transformovaných datech provádět rovnocenně.

Nepřesnost výsledků lze vyjádřit i tak, že každému žákovi je kromě jediného čísla jako úrovně jeho schopností (získané metodou maximální věrohodnosti) přiřazena ještě pětice čísel. Různost těchto čísel vystihuje neurčitost výsledku a umožňuje ji v analýzách kvantifikovat, čímž se předejde nesprávným závěrům. Tyto odhady se v literatuře označují jako plausible values, v této zprávě používáme český pojem „možné hodnoty“.

Obvykle se pak postupuje takto:

Každá analýza či charakteristika se provede pětkrát, pokaždé s jinou sérií možných hodnot.
Výsledek se získá aritmetickým průměrováním zjištěných údajů.

Indexy

Podobně, jako se vyjadřuje míra dovedností žáka v určité oblasti číselně, bylo by užitečné vyjádřit číslem i úroveň zázemí žáka, jeho aspirace, jeho postoje, jeho vztah k určitému problému či předmětu apod. Údaje o zázemí, aspiracích apod. sice respondent vyplňuje v dotazníku, avšak zpravidla jde o velké množství údajů, které je obtížné (kvůli velkému objemu dat) přímo použít ve statistických analýzách. Tato potíž se řeší vytvořením bloků otázek zaměřených na podobné téma (například se zkoumá míra souhlasu dotazovaného s různými výroky zaměřenými na stejnou problematiku). Sestava jednotlivých odpovědí respondenta na blok podobných otázek se pak převede na číslo (resp. několik čísel) vyjadřující celkový postoj respondenta k dané problematice. Takové číslo se pak nazývá index a označuje se charakteristikou oblasti, z níž pocházely otázky dotazníku (odpovědi na něž se pak převedly na index). Máme tak například index četnosti používání internetu, index motivace v přírodních vědách nebo index kulturního vybavení domácnosti.

Redukcí mnoha odpovědí na jediné číslo přirozeně dochází k určité ztrátě informace (zejména jsou poněkud potlačovány atypické kombinace odpovědí, takoví respondenti jsou pak řazeni do oblasti průměrné hodnoty indexu, ačkoliv se vlastně od průměru zásadně liší). Velikost ztráty závisí na tom, jak dobře a konsistentně jsou konstruovány otázky v bloku. Další slabinou, která se projeví až u složitějších analytických postupů, jsou omezené možnosti předpokladů o statistických a pravděpodobnostních vlastnostech indexů (nelze například automaticky předpokládat, že index má normální rozdělení). Praktický přínos je však značný, neboť ve statistických analýzách je mnohem lépe použitelný index než posloupnost odpovědí.

V některých případech je zkoumaná oblast natolik rozsáhlá, že se odvozují indexy pro její různé aspekty. Pak je možné z jednotlivých dílčích indexů konstruovat celkový index, resp. několik indexů popisujících zkoumané oblasti globálně. K tomu se však už používají jiné postupy, například faktorová analýza.

Variabilita, lineární model, čistý vliv faktoru

Zjišťujeme-li hodnotu nějaké veličiny (kvantitativního znaku) u více jedinců, obvykle taková veličina nabývá pro různé jedince různých hodnot. Vykazuje tedy variabilitu (česky můžeme říci „proměnlivost“). Variabilitu lze přitom vyjádřit i číselně jako součet druhých mocnin odchylek od průměrné hodnoty, tedy pomocí vzorce

\( SSq = \sum_{i=1}^{n} (Z_i - \bar{Z})^2 \)

kde Z1, Z2,… jsou zjištěné hodnoty veličiny a barZ je jejich aritmetický průměr.
Pokud lze ovšem jedince rozdělit do několika skupin podle jiného, kvalitativního znaku (např. pohlaví, vzdělání, kraj apod.), lze pro každou skupinu spočítat samostatný aritmetický průměr a v uvedeném vzorci jej použít místo společného:

\( SSq' = \sum_{i=1}^{n} \left( Z_i - \bar{Z}_{(k)} \right)^2 \)

kde Z1, Z2,… jsou zjištěné hodnoty veličiny a barZ je aritmetický průměr přidělený každé hodnotě podle toho, do které skupiny patří příslušný jedinec.

Je celkem logické, že průměry, které jsou počítány pro menší skupiny pozorování, se k těmto pozorováním přimykají těsněji než jeden společný průměr. Proto bude platit, že součet odchylek od společného průměru SSq bude větší (případně nanejvýš stejný) než součet odchylek od průměrů po skupinách SSq'. Použitím kvalititavního znaku pro rozdělení do skupin a výpočet jednotlivých průměrů došlo k redukci (zmenšení) variability. Říkáme též, že použitý kvalitativní znak „vysvětlil část celkové variablity“. Zmenšení se uvádí též v procentech.

Pokoušíme-li se zjistit vliv několika různých faktorů na určitou veličinu (tj. „vysvětlit“ veličinu pomocí daných faktorů), můžeme se dostat do problémů s interpretací výsledků v případě, kdy mezi vysvětlujícími faktory existuje nějaká souvislost (korelace). Například se může ukázat, že se mezi sebou významně liší výsledky žáků v určitých krajích; a také, že se významně liší výsledky žáků podle jejich socio-ekonomicko-kulturního statusu. Je ovšem známo, že socio-ekonomicko-kulturní status žáků se v různých krajích liší. Na místě je pak otázka, zda odlišnosti mezi různými kraji nejsou zprostředkovány právě pouze různým socio-ekonomicko-kulturním statusem žáků. Jinými slovy, zda by i po očištění od vlivu socio-ekonomicko-kulturního statusu zůstala v datech ještě nějaká zbytková závislost výsledku žáka na konkrétním kraji.

Analýzu současného působení většího množství faktorů na jednu veličinu lze účinně provést pomocí lineárního modelu. Ten zjišťuje, jak který faktor ovlivňuje vysvětlovanou veličinu a zda některé faktory nejsou zastupitelné jinými. Lineární model předpokládá, že vysvětlovaná veličina je kvantitativní – pokud tomu tak není, lze pomocí speciálních postupů analyzovat jako vysvětlovanou veličinu i proměnnou nabývající pouze dvou hodnot.

Hlavními výstupy analýzy pomocí lineárního modelu jsou

rozklad variability vysvětlované veličiny mezi jednotlivé faktory (tedy zjištění, jak velkou část proměnlivosti vysvětlované veličiny ovlivňuje ten který faktor), případně informace, že některé faktory lze z modelu vyloučit, protože jejich vliv není statisticky významný;
konkrétní koeficienty náležící jednotlivým úrovním faktorů, případně určující vliv spojitých faktorů .

Zmíněné koeficienty vyjadřují čistý vliv každého faktoru na vysvětlovanou veličinu, tedy po očištění od zprostředkujícího vlivu všech ostatních faktorů. Z toho lze tudíž usoudit, jak který faktor, resp. jeho úrovně, skutečně ovlivňuje vysvětlovanou veličinu. Aby bylo možné porovnat vliv kvalitativních faktorů se spojitými, uvádíme v této zprávě u spojitých faktorů vždy koeficient odpovídající změně spojitého faktoru o jednu směrodatnou odchylku.

Důležitým prvkem lineárního modelu je pořadí faktorů. Analýza totiž probíhá hierarchicky, takže faktor, je-li zařazen na začátku, vyčerpá pravděpodobně větší část variability, než kdyby byl zařazen na konci. Z toho vyplývá, že pořadí faktorů musí být stanoveno logicky s ohledem na skutečnou situaci.

Lineární model umožňuje analýzu i v situaci, kdy jednotlivá pozorování mají různé váhy.

Očekávaný výsledek

Známe-li u jedince některé nebo všechny hodnoty faktorů, můžeme sečtením hodnot odpovídajících koeficientů lineárního modelu zjistit, jaká hodnota vysvětlované proměnné příslušné kombinaci faktorů odpovídá. Takto vypočtená hodnota se nazývá očekávaným výsledkem (fitted value). Skutečný výsledek žáka se od očekávaného může samozřejmě lišit, koeficienty jsou však spočteny tak, aby celková odchylka skutečného a očekávaného výsledku byla co nejmenší.

Logistická regrese a logity

V případě, že potřebujeme zjistit současný vliv několika faktorů na určitou veličinu, ale tato veličina nabývá pouze dvou hodnot (tzv. binární či dichotomická), nelze užít klasický lineární model. V těchto případech se běžně užívá model logistické regrese. Tento model se snaží zjistit, na čem závisí pravděpodobnost, že respondent uvede určitou odpověď (souhlas, aspiraci na VŠ apod.). Model také umožňuje odhadovat pravděpodobnost určité odpovědi pro různé typy osob. Protože modelovat pravděpodobnosti přímo ze statistického hlediska nelze (jde o hodnoty pouze v intervalu 0 až 1), jsou pravděpodobnosti převedeny na tzv. logity pomocí vzorce

\( \text{logit} = \ln\left( \frac{p}{1 - p} \right) \)

Logity mají z matematického hlediska lepší vlastnosti než původní pravděpodobnost, např. nabývají hodnot na celé reálné ose.

Faktorová analýza

V některých situacích je k dispozici za každého jedince několik číselných údajů, přičemž lze předpokládat, že všechny nebo velká část z nich je významně ovlivněna stejnou veličinou. Například na výsledky několika testů z různých předmětů mohou mít vliv obecné předpoklady žáka ke studiu, jeho motivace, pozornost apod. Cílem faktorové analýzy je co nejlépe odhadnout hodnotu veličiny, která stojí za měřenými výsledky a kterou jako takovou přímo měřit nelze.

Pomocí faktorové analýzy lze odhadovat i více než jednu takovou veličinu, přesný počet odhadovaných veličin lze stanovit předem v podstatě libovolně podle kontextu situace. Například při konstrukci globálního (souhrnného) indexu pro danou oblast z několika dílčích indexů se použije faktorová analýza s odhadem pouze jediné veličiny. Nicméně existují i metody, které prověří, zda počet odhadovaných veličin je již dostatečný pro vyčerpání celé informace z údajů, jež jsou k dispozici.

Výstupem faktorové analýzy je kromě odhadnutých hodnot neznámé veličiny či neznámých veličin i tzv. faktorová matice, která popisuje míru působení odhadnutých veličin na jednotlivé známé číselné údaje. Podle toho, na jaké údaje neznámá veličina převážně působí, je možné jí přidělit charakteristiku. Například v PISA 2006 byly pomocí faktorové analýzy z 13 dílčích indexů vztahu žáka k přírodním vědám odhadnuty hodnoty tří veličin a podle působení každé z veličin na jednotlivé dílčí indexy dostaly odhadované veličiny své názvy (index orientace na přírodní vědy, index informovanosti v přírodních vědách a index vnímání užitečnosti přírodních věd).