Item-response theory (IRT)

Item-response theory (v češtině „teorie odpovědi na položku“, nejpoužívanější je ovšem zkratka IRT) je rodina matematických modelů, které umožňují použít jednotnou škálu pro různé testy a definují způsob přepočtu výsledků každého testu na jednotnou škálu.

Dále vycházejí z předpokladů, že:

testové položky měří u respondenta míru jedné stejné vlastnosti (tzv. latenci)
latence je spojitá veličina na nekonečné škále se středem v nule
odpovědi stejného respondenta v různých položkách jsou nezávislé
charakteristiky (parametry) položek jsou nezávislé na konkrétní osobě respondenta i na ostatních položkách testu

K těmto předpokladům se často přidává předpoklad, že latence má v populaci standardní normální rozdělení, tj. s nulovou střední hodnotou a rozptylem jedna.
Základní modely IRT sledují jednu latenci u každého respondenta pomocí dichotomických položek (Raschův model, dvouparametrický model, tříparametrický model a další) nebo pomocí polytomických položek (rating scale model, partial credit model, graded response model a další). Složitější modely mohou sledovat i více vlastností (více latencí) najednou.

Výpočty IRT jsou technicky složité, protože odhadují, jaká latence nejlépe odpovídá konkrétní sérii odpovědí respondenta v položkách testu. Pokud u některých nebo všech položek nejsou předem známy jejich parametry (není provedena kalibrace), pak se současně s latencemi odhadují i parametry položek. K tomu se obvykle používá metoda maximální věrohodnosti.

Z modelů IRT vyplývá, že nepřesnost odhadu latence není stejná pro všechny respondenty, ale lze ji stanovit individuálně.

Raschův model

Raschův model je nejjednodušším modelem item-response theory (IRT) pro dichotomické položky. Každá položka je charakterizována jedním parametrem, a to svou obtížností. Při respondentově latenci θ a obtížnosti položky b je pravděpodobnost, že tento respondent tuto položku úspěšně vyřeší, vyjádřena rovnicí modelu:

$ P(θ; a; b) = {e^{θ–b} \over 1+ e^{θ–b}} $

kde $ e $ je Eulerovo číslo.

Z rovnice modelu vyplývá, že respondent, jehož latence je rovna obtížnosti položky, má 50% pravděpodobnost jejího úspěšného vyřešení.

Raschův model lze alternativně zapsat takto:

$ P(θ; b) = {e^{θ+β} \over 1+ e^{θ+β}} $

Při tomto zápisu se parametru β říká snadnost položky (easiness). Platí $ b = – β $

Nevýhodami Raschova modelu jsou:

předpoklad stejné diskriminace všech položek, tj. že pravděpodobnost, že lepší žáci budou úlohu řešit lépe než horší žáci, bude u všech položek stejná,
opomenutí možnosti, že žák správnou odpověď uhodne (typická situace pro položky multiple-choice – s výběrem odpovědi z nabídky).

Uvedené nevýhody odstraňuje použití dvouparametrického a tříparametrického modelu.

Dvouparametrický IRT model

Dvouparametrický model item-response theory je zobecněním Raschova modelu. Stanovuje u každé položky kromě obtížnosti b i diskriminaci a. Při respondentově latenci θ, obtížnosti položky b a diskriminaci a je pravděpodobnost, že tento respondent tuto položku úspěšně vyřeší, vyjádřena rovnicí modelu:

$ P(\theta; a; b) = \frac{e^{\theta - b}}{1 + e^{\theta - b}} $

kde $ e $ je Eulerovo číslo.

Z rovnice modelu vyplývá, že respondent, jehož latence je rovna obtížnosti položky, má 50% pravděpodobnost jejího úspěšného vyřešení. Čím je a vyšší, tím rychleji se při změně latence mění pravděpodobnost úspěšného vyřešení.

Je-li diskriminace nulová, nezávisí pravděpodobnost úspěšného vyřešení na latenci – taková položka tedy nijak nesouvisí s měřenou vlastností. Položka s nulovou diskriminací je v testu nežádoucí, protože test prodlužuje, ale nepřináší žádnou informaci o latenci.

Je-li diskriminace záporná, jsou v položce úspěšnější respondenti s nižší latencí a méně úspěšní respondenti s vyšší latencí. Pro odhad latence však není podstatné, zda je diskriminace kladná, nebo záporná, neboť metoda odhadu latence ve dvouparametrickém modelu dokáže vytěžit informaci i z položek se zápornou diskriminací.
Dvouparametrický model lze alternativně zapsat takto:

$ P(\theta; a; b) = \frac{e^{\theta + \beta}}{1 + e^{\theta + \beta}} $

Při tomto zápisu se parametru $ β $ říká snadnost položky (easiness). Platí $ b = – aβ $.

Nevýhodou dvouparametrického modelu je opomenutí možnosti, že žák správnou odpověď uhodne (typická situace pro položky multiple-choice – s výběrem odpovědi z nabídky).

Tuto nevýhodu odstraňuje použití tříparametrického modelu.

Tříparametrický IRT model

Tříparametrický model item-response theory je zobecněním Raschova modelu a dvouparametrického modelu IRT. Stanovuje u každé položky kromě obtížnosti b a diskriminace aa ještě pravděpodobnost uhodnutí c. To znamená, že pravděpodobnost správného vyřešení položky u každého respondenta je nejméně rovna c. Při respondentově latenci θ, obtížnosti položky b, diskriminaci aa a pravděpodobnosti uhodnutí cc je pravděpodobnost, že tento respondent tuto položku úspěšně vyřeší, vyjádřena rovnicí modelu:

$ P(\theta; a; b; c) = c + \frac{(1 - c) \, e^{\theta - b}}{1 + e^{\theta - b}} $

Z rovnice modelu vyplývá, že respondent, jehož latence je rovna obtížnosti položky, má pravděpodobnost jejího úspěšného vyřešení rovnu $ c + (1–c)/2 $ Čím je $a$ vyšší, tím rychleji se při změně latence mění pravděpodobnost úspěšného vyřešení.

Je-li diskriminace záporná, jsou v položce úspěšnější respondenti s nižší latencí a méně úspěšní respondenti s vyšší latencí. Pro odhad latence však není podstatné, zda je diskriminace kladná, nebo záporná, neboť metoda odhadu latence ve tříparametrickém modelu dokáže vytěžit informaci i z položek se zápornou diskriminací.

Tříparametrický model, podobně jako dvouparametrický, dokáže vytěžit informaci i z položek se zápornou diskriminací.

Tříparametrický model lze alternativně zapsat takto:

$ P(\theta; a; b; c) = c + \frac{(1 - c) \, e^{\theta + \beta}}{1 + e^{\theta + \beta}} $

Při tomto zápisu se parametru $β$ říká snadnost položky (easiness). Platí $ b = – aβ $.

Nevýhodou tříparametrického modelu je značná výpočetní náročnost a nestabilita odhadu parametrů. Jeho používání bez další kontroly jeho výstupů může vést ke zkresleným závěrům.

Rating scale model

Rating scale model item-response theory je zobecněním Raschova modelu pro polytomické položky. Nad rámec Raschova modelu a obecných předpokladů IRT se v něm předpokládá, že:

všechny položky mají stejný počet možných hodnocení odpovědí a tato hodnocení jsou celočíselná od nuly výš,
rozdíly obtížností mezi sousedními stupni hodnocení nemusejí být stejné (tj. přechod od hodnocení 2 k hodnocení 3 nemusí být stejně obtížný jako přechod od hodnocení 1 k hodnocení 2),
rozdíly obtížností mezi různými hodnoticími stupni jsou ve všech položkách testu stálé (tedy přechod od hodnocení 2 k hodnocení 3 je stejně obtížný v první i ve čtvrté položce testu).

Při respondentově latenci θ, obtížnosti položky b a prazích přechodu do vyššího hodnocení ω(k) je pravděpodobnost, že respondent získá v položce hodnocení h, vyjádřena rovnicí modelu:

$ P(h; \theta; b; \omega) = \frac{P_h}{\sum_{k=0}^{K} P_k} $

Nevýhodou rating scale modelu je požadavek, že přechody mezi stupni jsou pro všechny položky stejně náročné. Zobecněním rating scale modelu jsou například partial credit model a graded response model.

Partial credit model

Partial credit model item-response theory je zobecněním Raschova modelu pro polytomické položky a zobecněním rating scale modelu. Nad rámec Raschova modelu a obecných předpokladů IRT se v něm předpokládá, že:

položky mohou mít různý počet možných hodnocení odpovědí (odlišnost oproti rating scale modelu), tato hodnocení jsou celočíselná od nuly výš,
rozdíly obtížností mezi sousedními stupni hodnocení se liší pro různé stupně hodnocení i pro různé položky (tj. přechod od hodnocení 2 k hodnocení 3 nemusí být stejně obtížný jako přechod od hodnocení 1 k hodnocení 2, přičemž v každé položce testu jsou tyto přechody obtížné jinak),
rychlost přechodu při změně latence respondenta je u všech položek stejná (položky mají stejnou diskriminaci).

Při respondentově latenci θ, obtížnosti položky b a prazích přechodu do vyššího hodnocení ω(k)ω(k) je pravděpodobnost, že respondent získá v položce hodnocení hh, vyjádřena rovnicí modelu:

$ P(h; \theta; b; \omega) = \frac{P_h}{\sum_{k=0}^{K} P_k} $

kde e je Eulerovo číslo a K je maximální hodnocení v dané položce; prahy ω(k) jsou různé pro všechny položky.

Nevýhodou partial credit modelu je požadavek na stejnou diskriminaci položek. Tuto nevýhodu odstraňuje např. zobecňující graded response model.

Graded response model

Graded response item-response theory je zobecněním dvouparametrického modelu pro polytomické položky a zobecněním partial credit modelu. Nad rámec dvouparametrického modelu a obecných předpokladů IRT se v něm předpokládá, že:

položky mohou mít různý počet možných hodnocení odpovědí (odlišnost oproti rating scale modelu), tato hodnocení jsou celočíselná od nuly výš,
rozdíly obtížností mezi sousedními stupni hodnocení se liší pro různé stupně hodnocení i pro různé položky (tj. přechod od hodnocení 2 k hodnocení 3 nemusí být stejně obtížný jako přechod od hodnocení 1 k hodnocení 2, přičemž v každé položce testu jsou tyto přechody obtížné jinak).

Při respondentově latenci θθ, obtížnosti položky b, diskriminaci aa a prazích přechodu do vyššího hodnocení ω(k)ω(k) je pravděpodobnost, že respondent získá v položce hodnocení hh, vyjádřena rovnicí modelu:

$ P(h; \theta; a; b; \omega) = \frac{P_h}{\sum_{k=0}^{K} P_k} $

Charakteristická křivka (funkce) položky

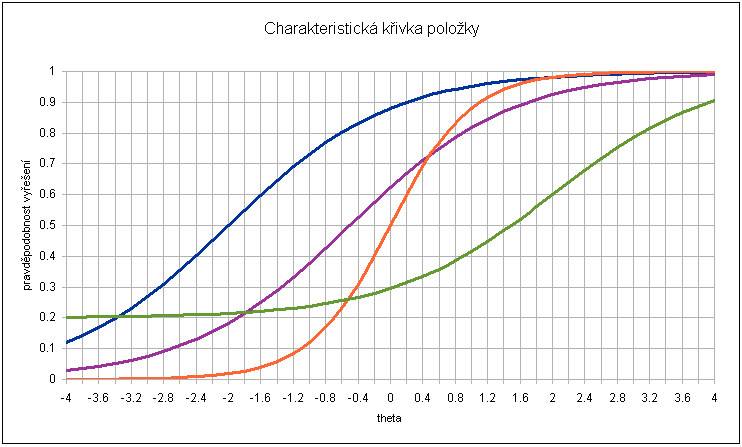
Modely IRT určují v každé položce vztah mezi latencí respondenta a pravděpodobností, že respondent položku vyřeší správně. Tento vztah se nazývá charakteristická funkce položky a jeho grafické znázornění charakteristická křivka položky (Graf 1).

Informační křivka (funkce) položky

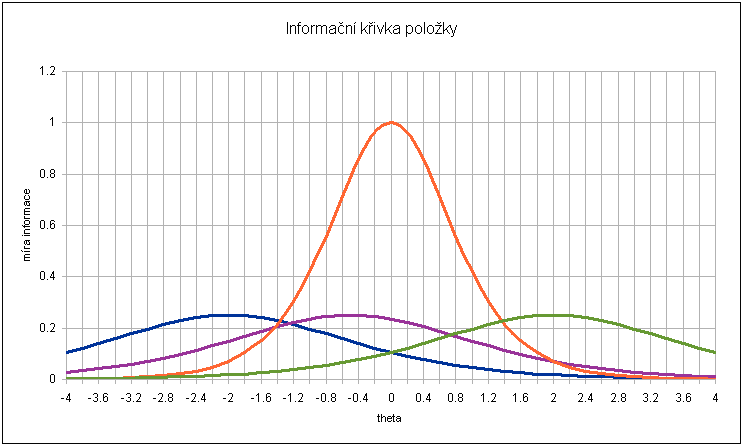
Přínos položek testu pro odhad latence je různý, liší se jak mezi položkami, tak mezi respondenty. Přínos je ovlivněn jednak diskriminací položky (schopností rozlišovat mezi lepšími a horšími, viz oranžová křivka s vyšší diskriminací), jednak přiměřenou obtížností pro respondenta. Vztah mezi přínosem a latencí u každé položky vyjadřuje informační funkce a jeho grafické znázornění se nazývá informační křivka položky (Graf 2).

Příklady křivek pro čtyři dichotomické položky

	modrá	fialová	oranžová	zelená
obtížnost	-2	-0,5	0	2
diskriminace	1	1	2	1
guessing				0,2

Graf 1

Graf 2

Informační křivka (funkce) testu

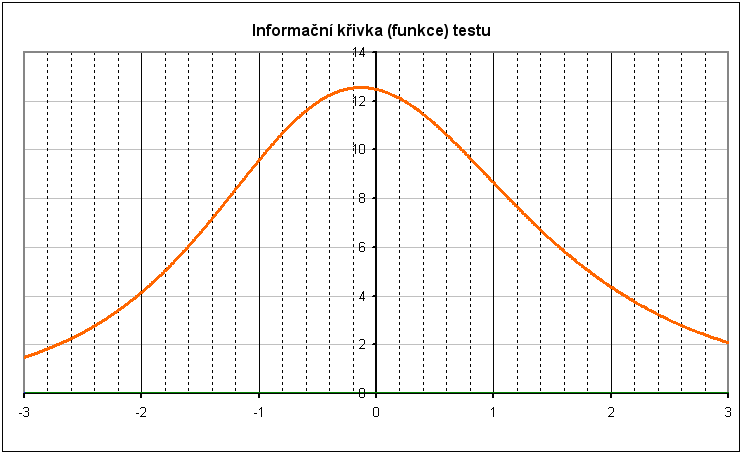
Přínosy jednotlivých položek testu pro odhad latence se sčítají. Vztah mezi úhrnným přínosem všech položek testu a latencí respondenta se nazývá informační funkce testu a je roven součtu informačních funkcí všech položek testu. Informační funkce testu má význam pro stanovení přesnosti odhadu latence.
Grafické znázornění informační funkce se nazývá informační křivka testu (Graf 3).

Přesnost odhadu latence

Směrodatná odchylka odhadu latence v modelech IRT se rovná odmocnině převrácené hodnoty informační funkce, tedy

$ SE(\theta) = \frac{1}{\sqrt{I(\theta)}} $

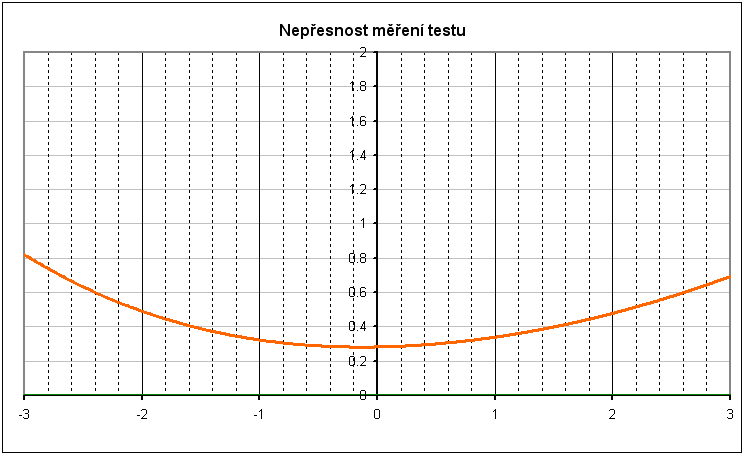
Směrodatná odchylka, a tedy nepřesnost odhadu se pro různé latence liší. Nejpřesnější odhad získáme pro respondenty, jejichž latence je v místě maxima informační funkce. Pro velmi nízké nebo velmi vysoké latence je přesnost odhadu velmi nízká (Graf 4).

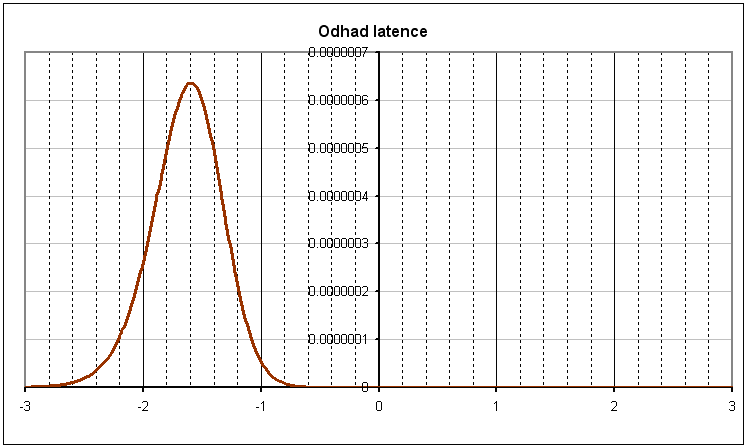
Latence se odhaduje pomocí metody maximální věrohodnosti a numerického hledání maxima funkce (Graf 5).

Příklad

Test má informační křivku znázorněnou Grafem 3 a nepřesnost odhadu latence znázorněnou Grafem 4. Graf 5 znázorňuje příklad věrohodnostní funkce určitého respondenta, maximum této funkce nastává v bodě –1,594. Tato hodnota je proto odhadem latence respondenta. Směrodatnou odchylku chyby odhadu latence pro tohoto respondenta lze odečíst z Grafu 4 a činí přibližně 0,4.

Graf 3

Graf 4

Graf 5